动态规划

动态规划有时被称为递归的相反的技术。递归是从顶部开始将问题分解，通过解决所有分解小问题的方式，来解决整个问题。而动态规划这是从底部开始解决问题，将所有小问题解决掉，然后合并成整体的解决方案，从而解决掉整个大问题。递归方式虽然很简洁，但是效率不高，但是不能说递归是不好的，本质上是，命令式语言和面向对象的语言对递归的实现不够完善，因为它们没有将递归作为高级编程特性。

动态规划方案通常使用一个数组来建立一张表，用于存放被分解成众多子问题的解。当算法执行完毕，最终的解法将会在这个表中找到。

先来看看最经典的斐波那契数列的递归解法：

递归解法

function fib(n){ 
    if(n < 2){
         return n; 
     }else{ 
         return fib(n - 1) + fib(n - 2); 
    } 
}

动态规划解法

function fibDyn(n) {
    var temp = [];
    for (var i = 0; i <= n; i++) {
        temp[i] = 0
    }
    if (n < 2) {
        return n;
    } else {
        temp[1] = 1;
        temp[2] = 1;
        for (var i = 2; i <= n; i++) {
            temp[i] = temp[i - 1] + temp[i - 2];
        }
        return temp[i-1];
    }
}

还有个比较经典的动态规划问题，给定两个字符串,求出它们的最长公共字串

我们回顾一下动态规划的解题思路：

• 从底部开始解决问题，将所有小问题解决掉，然后合并成一个整体的解决方案。
• 使用一个数组建立一张表，用于存放被分解成众多子问题的解。

最小的是每个字符，所以要把分解成单个的字符去匹配每个单个的字符。思路如下

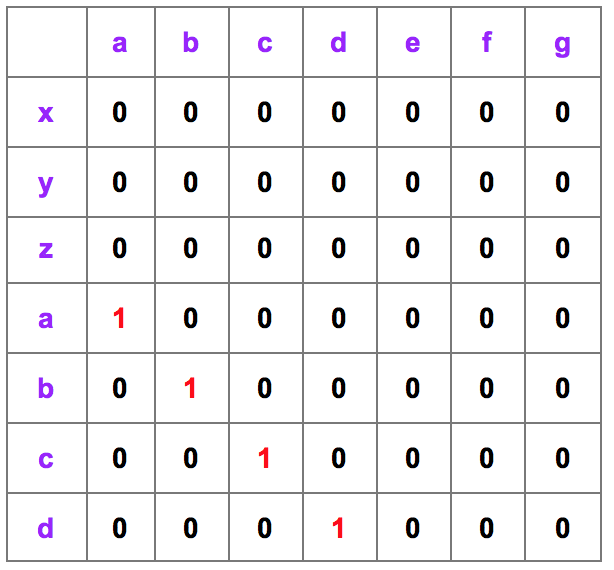
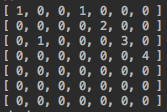
匹配为1，不匹配为0，这个时候我们就分解成为每个字符的匹配情况，由此得到。

function LCS(str1, str2) {
    var arr = []
    var maxLen = 0
    var index = 0
    for (var i = 0; i < str1.length; i++) {
        arr[i] = []
        for (var j = 0; j < str2.length; j++) {
            arr[i][j] = 0
        }
    }
    for (var i = 0; i < str1.length; i++) {
        for (var j = 0; j < str2.length; j++) {
            if (str1[i] == str2[j]) {
                if (i == 0 || j == 0 || (str1[i - 1] != str2[j - 1])) {
                    arr[i][j] = 1
                } else if (str1[i - 1] == str2[j - 1]) {
                    arr[i][j] = arr[i - 1][j - 1] + 1;
                }
            }
            if (arr[i][j] > maxLen) {
                maxLen = arr[i][j];
                index = i;
            }
        }
    }
    if (maxLen == 0) {
        return ""
    } else {
        var s = str1.slice(index+1-maxLen, index+1)
        return s
    }
}
var str1 = "abcdefg";
var str2 = "aczabcd";
LCS(str1, str2) // abcd