最小编辑距离

发表于
问题描述

给定 2 个字符串 a, b. 编辑距离是将 a 转换为 b 的最少操作次数，操作只允许如下 3 种：

  1. 插入一个字符，例如：fj -> fxj
  2. 删除一个字符，例如：fxj -> fj
  3. 替换一个字符，例如：jxj -> fyj
思路

用分治的思想解决比较简单，将复杂的问题分解成相似的子问题

  • 假设字符串 a, 共 m 位，从 a[1] 到 a[m]

  • 字符串 b, 共 m 位，从 b[1] 到 b[n]

  • d[i][j] 表示字符串 a[1]-a[i] 转换为 b[1]-b[i] 的编辑距离

那么有如下递归规律（ a[i] 和 b[j] 分别是字符串 a 和 b 的最后一位）：

  1. 当 a[i] 等于 b[j] 时， d[i][j] = d[i-1][j-1] , 比如 fxy -> fay 的编辑距离等于 fx -> fa 的编辑距离
  2. 当 a[i] 不等于 b[j] 时， d[i][j] 等于如下 3 项的最小值：
    • d[i-1][j] + 1（删除 a[i] ）， 比如 fxy -> fab 的编辑距离 = fx -> fab 的编辑距离 + 1
    • d[i][j-1] + 1（插入 b[j] )， 比如 fxy -> fab 的编辑距离 = fxyb -> fab 的编辑距离 + 1 = fxy -> fa 的编辑距离 + 1
    • d[i-1][j-1] + 1（将 a[i] 替换为 b[j] ）， 比如 fxy -> fab 的编辑距离 = fxb -> fab 的编辑距离 + 1 = fx -> fa 的编辑距离 + 1

递归边界：

  1. a[i][0] = i , b 字符串为空，表示将 a[1]-a[i] 全部删除，所以编辑距离为 i
  2. a[0][j] = j , a 字符串为空，表示 a 插入 b[1]-b[j] ，所以编辑距离为 j
代码

按照上面的思路将代码写下来

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
 int edit_distance(char *a, char *b, int i, int j)
{
    if (j == 0) {
        return i;
    } else if (i == 0) {
        return j;
    // 算法中 a, b 字符串下标从 1 开始，c 语言从 0 开始，所以 -1
    } else if (a[i-1] == b[j-1]) {
        return edit_distance(a, b, i - 1, j - 1);
    } else {
        return min_of_three(edit_distance(a, b, i - 1, j) + 1,
                            edit_distance(a, b, i, j - 1) + 1,
                            edit_distance(a, b, i - 1, j - 1) + 1);
    }
}

edit_distance(stra, strb, strlen(stra), strlen(strb));

但是有个严重的问题，就是代码的性能很低下，时间复杂度是指数增长的

上面的代码中，很多相同的子问题其实是经过了多次求解，解决这类问题的办法是用动态规划思想优化时间复杂度

像以上解决思路，是从后往前算的，比如我想知道 edit_distance(a, b, i, j) 我可能需要知道 edit_distance(a, b, i-1, j-1) ,有一种想法不错，就是从前往后算，先算出各个子问题，然后根据子问题，计算出原问题， 对于这个问题性能不错，而且也挺容易理解，下面就来说一说
例如以字符串 a = “fxy”, b = “fab” 为例

  1. 首先建立一个矩阵，用来存放子问题及原问题的编辑距离，并将递归边界在矩阵中填好，如下：

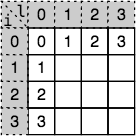
alt text

  1. 然后计算 i = 1, j = 1 所对应的编辑距离：比较 a[i] 和 b[j] 是否相等然后根据递归规律算出这个值
    比如在这种情况下 a[i] = f 和 b[j] = f , 那么 d[i][j] 就等于 d[i-1][j-1] 等于 0，然后计算 i = 1, j = 2 直到算出 i = 3, j = 3, 原问题的编辑距离就等于 d[3][3] ，最终矩阵如下：

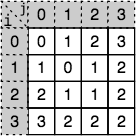
alt text

现在的时间复杂度已到了可接受范围，为 O(mn)

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
function minDistance(s1, s2) {
    const len1 = s1.length
    const len2 = s2.length

    let matrix = []

    for (let i = 0; i <= len1; i++) {
        // 构造二维数组
        matrix[i] = new Array()
        for (let j = 0; j <= len2; j++) {
            // 初始化
            if (i == 0) {
                matrix[i][j] = j
            } else if (j == 0) {
                matrix[i][j] = i
            } else {
                // 进行最小值分析
                let cost = 0
                if (s1[i - 1] != s2[j - 1]) { // 相同为0，不同置1
                    cost = 1
                }
                const temp = matrix[i - 1][j - 1] + cost

                matrix[i][j] = Math.min(matrix[i - 1][j] + 1, matrix[i][j - 1] + 1, temp)
            }
        }
    }
    return matrix[len1][len2] //返回右下角的值
}

minDistance('jary','jerry') // 2